News & Events

Weak value measurements by a strong duo

Assistant Professor Andrew Jordan and Associate Professor John Howell teamed up this past year with collaborators to make three strong advances related to weak value measurements and slow light. First, they discovered that gravity can push slow light down by about 1 Angstrom in the lab. Second, they demonstrated an optical pi cross-phase modulation jump. And third, they were able to measure extremely small (560-femtoradian) shifts of an optical beam. Much of this work merged Jordan's theoretical research with weak value measurements and Howell's experimental research with slow light and optical systems.

Publishing three papers between October 2008 and April 2009, their work was jump started when Howell posed an idea about gravitational deflection and slow light. Jordan and graduate student Justin Dressel hammered out the mathematics, then worked with slow light expert Howell and gravity expert Professor Sarada Rajeev to smooth out the details.

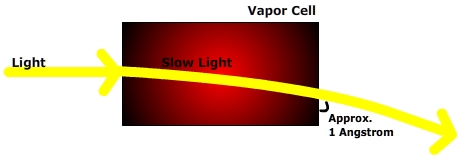
In their paper called "Gravitational Red-Shift and Deflection of Slow Light" (Physical Review Letters A 79, 013834, 2009), the four physicists describe how to set up an experiment that could measure the effect of gravity on slow light using a table-top device. This theoretical paper shows mathematically that, in a weak field limit, gravity causes a red-shift in optical frequency, which the slow light converts into a spatially varying index of refraction. This causes the light ray to bend in the medium, dropping by about 1 Angstrom. Using weak value measurements, the paper explains how to amplify and then detect this phenomenon.

(Figure 1)

As Jordan explains, "One of the first tests of the General Theory of Relativity was the confirmation of the bending of light near the sun in 1919, showing the effect of gravity on the propagation of light. However, given that gravity is a rather weak effect and that light typically travels at large speeds, any measurement of the gravitational effect has required a large propagation distance, much larger than we can manage in a typical laboratory."

(left, Justin Dressel; right, Sarada Rajeev)

For Earth-confined experiments, the dominant measurable effect of gravity on light is the gravitational red-shift of the frequency, not the bending of the light's trajectory. In the 1960's, physicists determined the effect of gravity on light traveling about 20 meters. The Rochester experiment, if realized as defined in the paper, could beat the previous height record by many orders of magnitude.

When put into a slow-light medium, the group velocity of the light slows down. The index of refraction varies steeply as a function of frequency, so in essence, the steepness of the slope determines the group velocity. But because frequency changes per the gravitational red-shift as height goes up, the index of refraction also varies as a function of height. This means that the slow-light medium operates somewhat like a lens, and it bends the light. As shown loosely in Figure 1 above, the slow-light medium creates a continuous gradation of index, with the acceleration depending on both the group velocity u_g and the phase velocity u_p of the light.

The effective gravitational acceleration is given by: g_eff = g u_p u_g / c²)

The equation of motion is the same as it would be when you drop a ball, but instead of:

g = 9.8 m/s²

we substitute g_eff

The group velocity is much less than the speed of light, so the effective gravitational acceleration (g_eff) is extremely tiny. But the time it takes the light to move through the medium is much longer than would be the case without the medium. Thus a wave packet drops much less due to gravity in a medium with slow group velocity than it would in a vacuum in the same amount of time, hence explaining, as the paper puts it, why the physicists did not observe wave packets "dropping like rocks in previous experiments."

After writing this paper, Howell began speculating about various ways to measure the angle of the bend in light. He read a paper by Paul Kwiat in Science (O. Hosten and P. Kwiat, Science 319, 787, 2008) that showed how to measure very sensitive deflections down to an Angstrom. He began thinking more about Jordan's work with weak value measurements. First, the two speculated about how to amplify the phase of light. They hoped to take a tenth of a degree and amplify it by a hundred using weak value measurements. But Jordan realized he could induce a 0-to-pi phase jump using cross polarizers. So rather than getting a phase amplification, they got a phase jump: it went from 0 to pi and nothing in between.

Basically, they used one beam of light to change the property of another beam. Working with Ryan M. Camacho, a former graduate student of John Howell's and now a postdoc at Caltech, Rochester graduate student P. Ben Dixon, and graduate student Ryan T. Glasser of Louisiana State University in Baton Rouge, Professors Jordan and Howell published their findings in Physical Review Letters ("Realization of an All-Optical Zero to Pi Cross-Phase Modulation Jump," PRL 102, 013902, 2009).

(left, P. Ben Dixon; right, Ryan Camacho)

Typically, beams of light don't interact; rather, the beams pass through each other. But when Jordan and Howell put two beams into a vapor cell, they found that one beam could change the phase of the other.

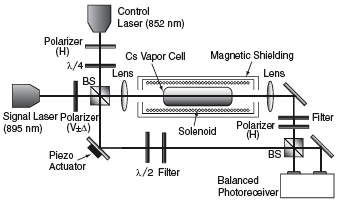
As shown in Figure 2, the signal laser beam passes through a vertically oriented polarizer. After passing through a beam splitter, one arm of the beam goes through a vapor cell and sets up an atomic dark state. The control laser beam induces a slight polarization rotation in the signal beam, which then passes through a second polarizer. The final state is post-selected by the second polarizer, and the phase of the post-selected signal beam is then measured by interference at the output beam splitter. The relative phase of the post-selected beam is always zero or pi.

(Figure 2)

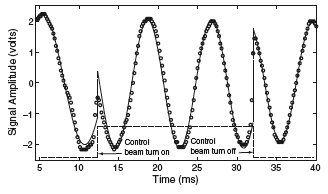
In Figure 3, when the control beam is turned on, the signal beam jumps out of phase. When the control beam is turned off, the signal beam jumps back in phase.

(Figure 3)

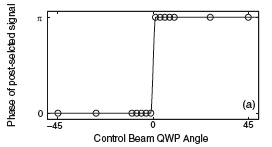
Another way to view this type of mechanism is shown in Figure 4. If one polarizer has a vertical orientation and the other a horizontal orientation, then light going between the two will never get through the second polarizer. But if you use a plate (labeled QWP, quarter-wave plate in the figure) to rotate the second polarizer a slight amount around the horizontal axis, a small amount of light will go through the second polarizer. You can see that the phase remains 0 until the quarter-wave plate angle is changed. Suddenly, there's a discontinuity, and the phase jumps to pi.

(Figure 4)

 Instead of using the quarter-wave plate, Jordan and Howell use the Cesium vapor cell to create a very weak field and induce a small cross-phase modulation, which then looks like a small rotation. After publishing the Physical Review Letters paper, Jordan and Howell turned their attention back to weak value measurements and amplification.

For this work ("Ultrasensitive Beam Deflection Measurement via Interferometric Weak Value Amplification," Physical Review Letters 102, 173601, 2009), they joined forces with graduate students P. Ben Dixon and David J. Starling. The paper's findings are so significant that PRL published it as a highlighted Editors Suggestion and also printed a Viewpoint article (Sandu Popescu,"Weak measurements just got stronger," April 27, 2009) about it.

Using an experimental setup as shown in Figure 5, the group was able to measure 560-femtoradian shifts of an optical beam, as well as measure the linear travel of a piezo actuator down to 20 femtoradians.

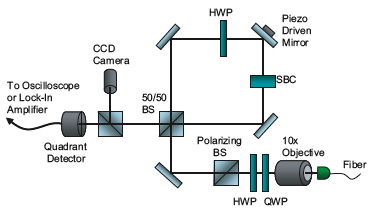
(Figure 5)

Here, a laser beam is collimated using a 10x microscope objective. The beam then passes through half and quarter-wave plates and a polarizing beam splitter, resulting in a pure horizontal polarization. Moving clockwise, the beam enters a Sagnac interferometer input port (marked SBC for Soleil Babinet compensator), which adds a tunable phase to the beam. The SBC is set to add this phase to vertically polarized beams relative to those polarized horizontally.

Moving counterclockwise, the beam first passes through the SBC, which now has no relative effect, then through the half-wave plate, changing the polarization to vertical. A piezo electric actuator scans the tilt of one of the interferometer mirrors back and forth, and the tilt of the mirror gives the two propagation directions opposite deflections.

Because the tilt of the mirror is so slight, it must be amplified before it can be measured. The amplification occurs due to the strong interference between the clockwise and counterclockwise beams and enables Howell and Jordan to measure the deflections of the piezo device down to roughly one picometer, which is roughly the size of a uranium nucleus. The amplification caused by the interference is up to 100 times larger than, say, one picometer.

Post-selection is achieved by monitoring the light that exits from the dark port of the interferometer. The Sagnac interferometer makes light travel in both directions for the same amount of time. Hence, a perfect constructive interference goes out the direction in which the light entered; and a perfect destructive interference should go out the dark port. But tuning the SBC to add a small but nonzero relative phase allows a small amount of light out of the dark port. The SBC and half-wave plate alters the phase of one path slightly from the phase of the other, essentially letting some light through what would have been the perfect destructive interference. This light passes through a beamsplitter and sent to a CCD camera and a quadrant detector. At the end, the researchers know whether the beam is tilted slightly toward the left or the right: this is the weak value measurement.

(lhg)